회귀분석을 공부하다보면 다중공선성(Multicollinearity)에 대해서 배우게 된다.
다중공선성은 회귀모형에서 설명변수들 간의 상관성이 클때, 그 설명변수의 회귀 계수의 불확실성, 즉 표준오차(Standard Error)가 필요 이상으로 커짐을 의미한다. 이것은 좀 더 쉽게 얘기하면, 회귀계수가 실제로 유의하지만 유의하지 않게 될 가능성이 커짐을 의미한다. 즉, 모형 자체가 너무 보수적으로 되는것이다.
나는 문득 다중공선성이 신뢰구간의 기능 자체를 깨뜨리는건 아닌가 하고 생각하게 되었다. 즉, 다중공선성으로 인해 본래 신뢰구간의 기능인 같은 데이터 발생 상황에서 100번 중에 95번은 신뢰구간이 모수값을 포함한다는 그 기능 자체가 망가지는 건 아닌가 하고 생각해보게 되었다. 그런데, 분명 내가 회귀분석을 배웠을 때에는 신뢰구간의 기능자체가 망가지는거라고 배우진 않았었다. 다만, 어떤 설명변수의 효과를 보이고 싶을 때, 그 설명변수의 회귀모수에 대한 신뢰구간이 너무 넓어져서 음수와 양수, 그리고 0을 모두 포함하게 되므로 사실상 이를 보일 수 없게 될것이라고 배웠었다.
그래서 개인적으로 실험을 좀 해보았다.
먼저 관측치 n을 100으로 하고,

과 같이 하여 진행하였다.
이때, 단순 선형 회귀분석 결과,

이 경우 , x1,x2,x3의 신뢰구간이 모두 회귀모수 1,2,3을 포함한다. (회귀계수는 정규분포를 따르므로, 회귀모수에 대한 신뢰구간은 (회귀계수 - 1.96 * 표준오차, 회귀계수 + 1.96*표준오차) 와 같이 나타낼 수 있다. )

Variance inflation factor(VIF) 역시 크지 않다. 위 데이터 생성과정을 1000번 반복하여, 1000번 중에 신뢰구간이 몇번이나 각 모수값을 포함하는지 확인하였다.
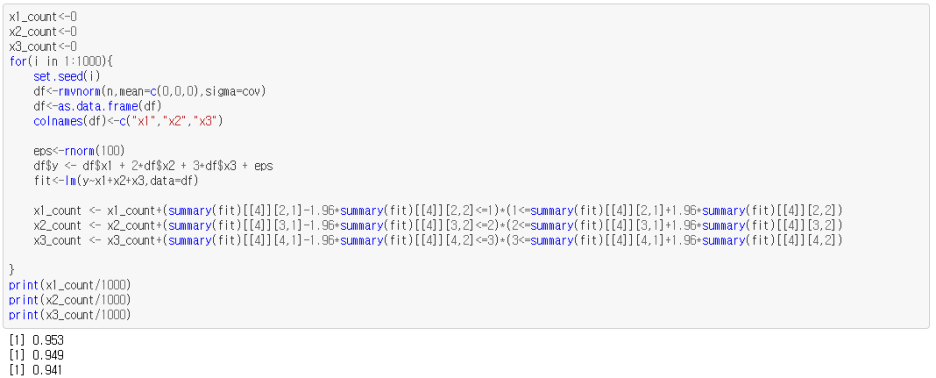
그 결과 각 회귀계수의 신뢰구간이 각 회귀모수를 950번에 가깝게 포함함을 확인하였다.
다중 공선성을 좀 더 심각하게 만들어서 위 과정을 반복해보았다. 즉, 아래와 같이 데이터 생성과정을 바꾸었다.
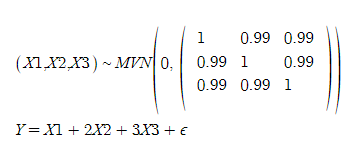
그랬더니, 처음 돌려본 케이스에서는 다음과 같이 나왔다.

즉, 이 경우에도 X1,X2,X3의 회귀모수에 대한 신뢰구간이 1,2,3을 포함함을 확인할 수 있다. 단, 이 경우에 각 회귀계수에 대한 표준오차는 0.8정도로 전에 다중공선성이 심하지 않았을 때 0.2 정도였던거에 비하면 증폭이 되었다.

VIF 역시 상당히 크게 나왔다. 즉, 다중공선성이 심각하다.

1000번 돌린 결과이다. 다중공선성이 심각하지 않았던 때와 동일하게 참 회귀모수를 포함하는 횟수는 950번과 가깝다. 그렇다면 0을 포함하는 횟수는 어떻게 될까? 회귀모수에 대한 신뢰구간이 0을 포함한다는 것은 거기에 대응되는 설명변수가 유의하지 않음을 의미한다. (이는 p-value가 0.05보다 크다는 것과 동치이기 때문이다.)
그 결과는 아래와 같다.

0을 포함하는 횟수가 x1의 경우 765번, X2의 경우 323번으로 상당히 많다.
그렇다면 다중공선성이 심하지 않았을 경우에는 어떨까?

다음과 같이 0을 포함하는 횟수가 x1의 경우는 12번, X2,X3의 경우에는 0번으로 현저히 줄어듬을 확인할 수 있었다.
본 실험결과를 요약하면 이러하다.
다중공선성이 심할 경우에 회귀모수에 대한 신뢰구간의 기능 자체가 무너지는 것은 아니다. 하지만, 그 구간의 길이 자체가 넓어지기 때문에 0을 너무 자주 포함하게 된다. 즉, 귀무가설을 기각을 해야 하는 상황인데도 기각을 너무 하지 않는다. 검정의 관점에서 보자면 1종오류는 정상적이지만 2종오류 자체가 너무 커지는 것이다.(검정력이 너무 약하다.) 그래서 실질적으로 분석을 할 때에는 다중 공선성을 피하고자 Ridge regression이나 PCA regression을 사용하게 된다.
하지만 다중공선성이 심함에도 어떤 변수의 효과가 유의하게 나왔으면 어떻게 할까?
일단, 다중공선성은 1종오류가 제어가 되는 상황이므로, 해당 경우에는 그 변수가 유의한것으로 판단하면 된다.
그렇지만 아마 그 변수에 대한 신뢰구간은 넓을 것이다. 다중공선성이 심각하면 발생되는 표준오차가 커지는 문제 (신뢰구간이 길어지는 문제)가 왜 문제가 되는지에 대한 포스팅은 아래 게시글에 있다.
https://raniche-note.tistory.com/2?category=1018664
위 글에 대한 자세한 코드는 아래 깃허브에 있습니다.
https://github.com/Minsoo1036/Experiment_about_Multicollinearity
'데이터 사이언스 > Statistics' 카테고리의 다른 글
| [통계학] 다중공선성은 정말로 예측력과 상관없을까? (0) | 2022.09.05 |
|---|---|
| 베이지안 시계열 모형 prophet (in Python) (1) | 2022.08.11 |
| 영화 "더플랜" 을 통해 배우는 통계검증의 심각한 오류 (0) | 2022.07.26 |
| [통계학] 베이지안적 사고와 빈도주의적 사고 (0) | 2022.06.14 |
| [통계학] 최대 가능도 추정량 (Maximum Likelihood Estimator)란? (0) | 2022.06.14 |