black-box 모델인 머신러닝의 예측값에 대한 설명 니즈가 커지고 있다.
이에맞추어 오늘은 XAI 방법론 중에 하나인 SHAP value 에 대해서 깊이 파보고자 한다.
경제학의 게임이론 분야에서 대가인 Lloyd Shapley(1951) 가 제안했던 Shapley Value의 개념을 머신러닝의 해석에 적용한 것이 SHAP Value 이다.
이러한 SHAP Value는 Su-In Lee 와 Scott Lundberg 가 2017년에 "A Unified Approach to Interpreting Model Predictions" 라는 제목의 논문으로 발표하였다.
Shapley value는 Efficiency, Dummy player, Symmetry, Strong monotonicity, Additivity 등의 지표로써 매력적인 성질들을 가지고 있다.
이에 따라 SHAP value 역시 머신러닝의 예측값에 대한 변수들의 contribution에 대한 measure로써 좋은 성질들을 가지고 있다.
SHAP value에 대해 본격적으로 들어가기에 앞서, Shpley value에 대해 좀 더 알아보자.
Shapley value (1951)
본래 Shapley Value는 팀플레이의 결과물로 나온 보상을 나눠가질때 각 팀원들에게 돌아갈 보상을 합리적으로 정하는데 그 목적이 있었다.
즉, 기여를 많이한 팀원에게 많은 보상이 돌아갈테고, 기여를 적게한 팀원에게 적은 보상이 돌아가게 될 것이다.
그리고 그러한 보상의 정도를 정량적으로 Shapley value를 통해 정할수 있는 것이다.
예를 들어보자. 3명의 팀원이 한 팀이 되어 상품을 판매한다고 해보자. 1달 후 상품이 100만개 팔렸다고 했을때 3명의 팀원들에게 돌아갈 보상은 어떻게 될까
가장 심플한 방식으로는 공산주의적 방식으로 3명 모두에게 전체 이익의 1/3씩 나눠주는 것이다.
하지만 이 팀원 5명이 각각 A,B,C 라고 할 때, A가 획기적인 방식을 고안해 상품을 비약적으로 많이 팔 수 있게 되었다고 쳐보자.
또한, 팀원 C는 한달간 몸이 아파 상품 판매에 거의 기여하지 못했다고 해보자. 이럴 경우에 어떻게 해야 합리적으로 팀원들에게 보상을 나눌 수 있을까
Shapley value는 가상의 실험을 통해 이 문제를 해결하고자 한다. 그 가상의 실험은 아래와 같다.
A의 기여도 계산을 위한 가상의 비교 실험 셋팅
1. ∅ vs. {A} from {A,B,C}
2. ∅ vs. {A} from {A,C,B}
3. {B} vs. {B,A} from {B,A,C}
4. {C} vs. {C,A} from {C,A,B}
5. {B,C} vs. {B,C,A} from {B,C,A}
6. {C,B} vs. {C,B,A} from {C,B,A}
위 실험 셋팅을 유심히 보면, 왼쪽 셋팅은 A가 없는 모든 경우들이며 오른쪽 셋팅은 왼쪽 셋팅에서 A가 추가로 들어간 경우들 임을 알 수 있다.
즉, 위 6가지 실험에서 오른쪽 집합 구성원이 협업했을 때와 왼쪽 집합 구성원이 협업했을 때 결과값(매출)의 차이는 각 경우에서 A의 기여도로 볼 수 있다.
결론적으로 말하면 이 A 의 기여도 6개를 평균낸다면 팀에서 A가 받아갈 보상을 구할 수 있게 된다. (또는 총 기여도를 구할 수 있게 된다)
위 실험셋팅은 위에 표시한 바와 같이 순열(from 뒤의 집합)로 쉽게 만들수 있다. 순열에서 A가 위치한 지점에 따라서 그 앞의 부분집합을 대조군으로 두는 방식으로 말이다.
예를들어, 첫번째와 두번째 실험에서의 순열 {A,B,C}, {A,C,B} 에서 순서상 A의 앞에 해당하는 부분집합은 공집합이므로 이와 대조비교한다.
그리고 세번째 실험의 경우 순열 {B,A,C} 에서 순서상 A의 앞에 해당하는 부분집합은 {B} 이므로 이와 대조비교하는 식이다.
이런식으로 계산해서 얻을 수 있는 이점은 실험에 참여하는 팀원의 개수에 따라 나누어 각각 평균한 뒤에 이들을 다시 평균냄으로써 팀원의 개수 조합에 의한 기여도의 inflation을 방지할 수 있다는 점이다.
위의 셋팅에서도 팀원이 0명인 경우, 1명인 경우, 2명인 경우 모두 2가지씩 실험이 진행되어 팀원의 명수에 따른 조합의 개수에 영향을 받지 않게 되었다.
이제 A의 Shapley Value를 계산해보자. v(S)를 S라는 집합의 기여도라고 하면, A의 Shapley Value는 아래와 같다.

한편, 이는 이렇게도 표현할 수 있다. (이는 A가 팀에서 받아가야할 보상의 양을 말한다.)
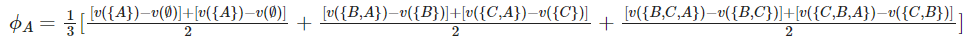
앞서 언급했듯, Shapley value는 구성원의 개수별로 평균을 낸 후에 이를 다시 평균한다.
위 식에서도 구성원이 0명인 case, 1명인 case, 2명인 case에 각각 A의 기여도를 평균하여 구한 후에 이를 다시 평균한 것을 알 수 있다.
물론 사실상 구성원이 0명인 case나 2명인 case는 두 실험이 같은 실험이긴 하다. 하지만 이렇게 인위적으로 순열을 통해 실험을 만들면 모든 경우에 대해서 예외없이 평균 기여도를 구할 수 있게 되며 단순히 구성원의 조합의 수가 많아지는 것에 의한 기여도 증폭을 방지할 수 있다.
즉, 구성원이 0명일 때, 1명일 때, 2명일 때 각각 A의 (대표)기여도를 산출한 뒤에 이를 평균하여 A의 총 기여도를 메기는 것이라고 볼 수 있다.
이러한 Shapley value를 좀 더 일반적인 식으로 표현하면 아래와 같다. (i 번째 구성원에 대한 Shaple value이다)

단, 위 식에서 N = {A,B,...} (모든 구성원들 집합) 이며 |N|은 그 집합을 구성하는 원소의 개수
Shapley value 에서 가장 매력적인 성질은 아마 efficiency 일 것이다. efficiency란 모든 구성원들의 Shapley value의 총합이 전체 구성원이 참여했을때 보상과 일치한다는 것이다. 즉, 위 예제에서 총매출 ϕA+ϕB+ϕC=v(A,B,C)=총매출 이 된다.
SHAP Value (2017, Application to ML)
이제 위 Shapley value를 머신러닝의 예측값 해석에 적용하는 방법에 대해 알아보자.
이를 위해서는 다소 통계적 개념들이 들어간다. 조건부 기댓값, 주변 기댓값, 몬테카를로 추정, causal inference에서 intervention에 대한 이해가 필요하다.
먼저 이전 섹션에 있던 Shapley value 계산식을 그대로 가지고 와보자.
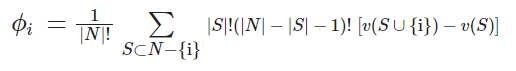
여기에서

으로 두면,
SHAP value를 계산할 수 있다.

실제로는 머신러닝 모델을 통해 구해지는 조건부 기댓값 f(Z)=E(Y|Z) 에 대한 추정치를 사용한다.
그리고 이를 통해 그 모델이 생각하는 그 변수의 기여도를 측정할 수 있게 된다.
즉, 아래 v(S)를 계산하기 위해서는 $$ Z_S $$ 의 분포는 고정해둔 채 $$ Z_S^{-} $$ 만을 랜덤 변수로 생각하여 기댓값을 구하는 것이다.
예를 들어, E(Y|X1,X2,X3)=f(X1,X2,X3) 라고 머신러닝 모델이 학습하였다고 하자.
그리고 하나의 관측치 x1=10,x2=5,x3=1 에 대하여 y의 예측값, 즉 E(Y|X1=10,X2=5,X3=1) 을 100이라고 예측했다고 치자.
이때 모델이 생각하는 x1=10 의 기여도(예측값 100에서 x1 이 차지하는 정도), 즉 SHAP value를 계산하기 위해서는 어떻게 할까
여기서 N = {1,2,3} 이 되며, i = 1 이 된다. 그리고 위 Shapley value 계산식에서 ∑ 안의 v(S∪{i}) 와 v(S) 는 집합 S와 x1을 현재 관측된 값으로 고정했을때와 고정하지 않았을때의 기댓값의 차이가 된다.
이 예제에서 S 는 {2,3}의 부분집합인 공집합, {2}, {3}, {2,3} 이렇게 4가지가 될 수 있다.
S가 공집합이라고 가정하면 v(S∪{i})=v({1}) 이 되며, v(S)=v(∅) 이 된다.
v({1}) 은 x1=10 으로 고정한 상태에서의 기댓값이 되며 여기서 다른 변수들은 랜덤 변수가 된다.
v(∅) 은 모든 변수들이 랜덤 변수인 상태에서의 기댓값이 된다.
Black Box 모델로 부터 이러한 기댓값을 얻어내기 위해서는 현실적으로 Monte Carlo 방법을 사용해야한다.
Monte Carlo 방법이란 평균으로 적분을 근사하는 것을 말하는데 이를 통해 기댓값을 표본에서 얻어지는 평균으로 추정할 수 있게 된다.
즉, v({1})을 구하기 위해서는 X1=10 으로 고정한 채로 X2 와 X3 를 해당 결합분포로 부터 랜덤 샘플링하여 그 샘플들에서 얻어지는 Y의 조건부 기댓값들을 평균 내어 추정할 수 있다.
마찬가지로, X1,X2,X3 를 해당 결합분포로 부터 랜덤 샘플링하여 그 샘플들에서 얻어지는 Y의 조건부 기댓값들을 평균내어 v(∅) 를 추정할 수 있다.
즉, 모델은 고정되어 있고 그 모델의 input만 이리 저리 바꾸어 비교함으로써 (한쪽은 X1을 상수로 고정, 한쪽은 X1 또한 랜덤변수로 생각) X1이 10이었기 때문에 가질 예측값에 대한 기여도를 measure하는 것이다.
그리고 여기서 결합분포를 추정해 샘플을 따로 추출할 필요는 없으며, 그저 우리에게 주어진 train data를 이용하면 된다.
즉, train data에서 X2와 X3 컬럼만 모아서 데이터를 본다면 그것이 X2, X3 의 결합분포로 부터 추출된 샘플과도 같다.
다시말하면, v({1}) 을 구하기 위해서는 train data에서 X1 컬럼만 전부 10의 값을 갖도록 만들고 X2 와 X3 컬럼은 그대로 사용하여 해당 샘플들에 대한 Y의 조건부 기댓값, 즉 E(Y|X1,X2,X3) 를 머신러닝을 통해 구해내어 이들을 평균내면 된다.
마찬가지로, v(∅) 을 구하기 위해서는 train data를 그대로 두고, 그냥 해당 샘플들에 대한 Y의 조건부 기댓값들을 머신러닝을 통해 구해서 이들을 평균내면 된다.
이런 방식으로 상수(실제값)로 고정할 조합을 정할 때, 한쪽은 X1 을 포함한 모든 조합, 다른 한쪽은 X1 을 포함하지 않은 모든 조합을 비교하여 가중평균하면 X1=10이 예측값 100에 대해 가지는 SHAP value를 계산할 수 있게 된다.
마찬가지 방식으로, X2=5,X3=1 이 예측값 100에 대해 가지는 SHAP value를 계산할 수 있게된다.
그리고 이들 세개의 SHAP value들과 intercept 항의 합산은 놀랍게도 100이 된다. (Shapley value의 efficiency 성질에 의해서)
=================================================
한편, SHAP value의 원본 버전 (2017년 논문에 적힌) 은 위와 조금 다르다.
원래는 X1=10 의 SHAP value를 구할 때, X2,X3 의 조건부 분포, 즉 X2,X3|X1=10 로 부터 구하도록 제시되었다.
하지만 https://www.amazon.science/publications/feature-relevance-quantification-in-explainable-ai-a-causal-problem 에 따르면 변수들의 진정한 기여도를 재기 위해서는 Causal Inference에서 자주 사용되는 개념인 Intervention 이 주어진것과 같은 관점으로 바라봐야한다고 한다.
즉, 한 변수의 기여도를 재기 위해서는 그 변수만 변했을 때의 영향도를 평가해야 하므로 다른 변수들이 그들간의 Association에 의하여 함께 바뀌는것을 피해야한다는 뜻이다.
이에 따라 Dominik Janzing, Lenon Minorics, Patrick Blöbaum 세 명의 저자들은 원본 SHAP value를 수정해야 한다고 주장했다.
그런데 아이러니 하게도 SHAP value의 원저자들도 X2,X3 의 조건부 분포는 실제로 구하기 어렵기 때문에 X2,X3 의 주변 결합 분포로 이를 근사하여 사용하는 것을 제안하고 이미 패키지 상용화를 해둔 상황이었다. (트리 기반의 Tree SHAP은 조건부 분포, 주변 결합 분포 버전 모두 가능하다)
그리고 이 근사하는 방식이 사실은 이론적으로 더 적합한 방식이라고 Dominik Janzing, Lenon Minorics, Patrick Blöbaum 저자들은 말한 것이다.
이에 대한 글은 SHAP value의 원저자인 Lundberg가 답변한 아래 깃허브 글에서도 확인할 수 있다.
오늘은 머신러닝에서 설명가능한 인공지능 기법으로 자주 쓰이는 SHAP value에 대해 이론적으로 심층있게 알아보았다.
다음 포스팅에서는 이러한 SHAP value를 파이썬에서 어떻게 사용할 수 있는지 실제 예제를 다루어 보려 한다.
'데이터 사이언스 > 머신러닝 & AI' 카테고리의 다른 글
| [딥러닝] 딥러닝에서 weight initialization 의 영향력 (0) | 2023.11.13 |
|---|---|
| 회귀문제에서 Random Forest, SVM, XGBoost 튜닝하는법 (in python) (1) | 2022.10.08 |
| 크로스엔트로피와 최대가능도추정량(MLE)간의 관계 (0) | 2022.08.17 |
| 엔트로피, 크로스엔트로피, 쿨벡라이블러 다이버전스 (0) | 2022.08.15 |
| 딥러닝과 머신러닝, 그리고 모수적 방법과 비모수적 방법이란 ? (0) | 2022.08.15 |