오늘은 시계열 데이터를 가지고 회귀분석을 돌릴때 종종 나타나는 가성 회귀(spurious regression)에 대해 써보고자 한다.
가성 회귀란 두 시계열 데이터 사이에 실제로는 인과관계가 없는데 시간적 우연성으로 인해 유의한 상관관계가 나타나는 것을 말한다.
가성 회귀의 예시들은 아래 링크에서 아주 잘 정리해놓았다.
http://mayoral.iae-csic.org/timeseries_insead/examplespurious.pdf
그 중 몇가지만 예시를 들어보자면
미국의 수출 인덱스와 호주의 남성 기대 수명은 유의한 수준의 양의 상관을 보였으며
미국의 R&D 지출과 남아프리카의 인구 간에도 유의한 수준의 양의 상관을 보였다.
즉, 두 시계열은 각자의 시간적 추세에 따라 증가했을 뿐인데 그 둘만 놓고 상관분석을 하거나 회귀분석을 하면 그 관계가 유의하게 판단이 되는 것이다.
위 예시와 같이 두 시계열이 비정상(non-stationary)일때 이러한 문제는 종종 일어나며, 심지어 stationary라고 하더라도 이
러한 문제가 완전히 해결되지는 않는다고 알려져 있다. (https://ideas.repec.org/p/pra/mprapa/59008.html)
(참고로 stationary와 non-stationary에 대한 개념은 아래 포스팅에서 확인할 수 있다.
https://raniche-note.tistory.com/66)
이를 직접 확인해보기 위해 실제로 R로 실험을 해보았다.
먼저, 두 non-stationary인 랜덤워크 A 와 B를 만든 후에 상관분석을 한 결과는 아래와 같다.
R코드)
s1 <- 100
s1_li <- c(s1)
for(i in 1:1000){
e <- rnorm(1,0,1)
s1_new <- s1_li[i] + e
s1_li <- c(s1_li, s1_new)
}
A <- s1_li #랜덤워크 A
s2 <- 10
s2_li <- c(s2)
for(i in 1:1000){
e <- rnorm(1,0,1)
s2_new <- s2_li[i] + e
s2_li <- c(s2_li, s2_new)
}
B <- s2_li #랜덤워크 B
cor.test(A,B) #상관분석
plot(A,type='l',ylim=c(0,200), main="original two random walks") #시각화
lines(B,col='blue')
결과)

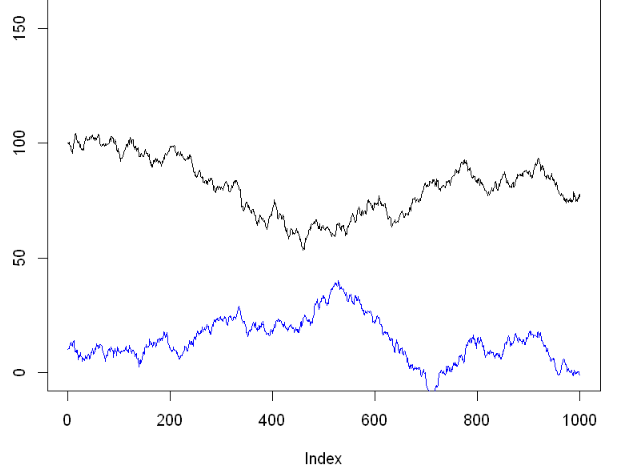
두 랜덤워크 A와 B는 서로 독립적으로 만들어져 인과관계가 실제로는 절대 있을수 없다.
하지만 상관분석 상으로는 두 시계열의 상관성이 유의하게 나타났다.
두 랜덤워크 A와 B를 회귀분석을 돌려보니 아래와 같은 결과가 나왔다.
R코드)
summary(lm(A~B))
결과)

R코드)
summary(lm(B~A))
결과)

A를 종속변수로 하든, B를 종속변수로 하든 두 회귀분석의 결과로만 봐서는 A와 B사이에 유의한 수준의 선형관계가 있는것으로 확인된다.
하지만 이는 시간적 우연성으로 인한 허위 상관 관계(spurious correlation)이며, 이를 판단하기 위해서는 잔차의 stationarity를 확인하는것이 중요하다고 알려져있다.
즉, 잔차의 stationarity가 만족이 되면 두 시계열 사이의 관계가 우연적인 시간적 추세로 인한 spurious 관계는 아니라는걸 밝히는 식이다. (그리고 이것이 우연적인 시간적 추세로 인한 spurious가 아니라고 하더라도 confounder로 인한 spurious 문제가 있을수도 있으니 주의가 필요하다. 이것과 관련된 포스팅은 추후에 진행해보도록 하겠다.)
위 상황에서도 두 회귀모형(A를 종속변수로 한 모형, B를 종속변수로 한 모형)의 잔차의 정상성을 확인해보았다.
먼저 시각적으로 확인한 코드는 아래와 같다.
R코드)
fit1 <- lm(A~B)
plot(resid(fit1),type='l')
결과)

R코드)
fit2 <- summary(lm(B~A))
plot(resid(fit2),type='l')
결과)

일단 육안으로 봤을때도 두 회귀모형의 잔차는 비정상(non-stationary)인것처럼 보인다.
이제 정상성 테스트를 통해 이를 통계적으로 검증해보도록 하겠다.
정상성 테스트로는 ADF(Augmented Dickey-Fuller) test 와 KPSS test를 사용하였다.
그 결과는 아래와 같다.

ADF test는 귀무가설이 기각되면 stationary라는것이 확인되며 반대로 KPSS test는 귀무가설이 기각되지 않아야 stationary라는것이 확인된다. 위 결과를 보면 두 회귀모형의 잔차 모두 ADF test의 귀무가설은 기각되지 않았으며 KPSS test의 귀무가설은 기각된 것을 확인할 수 있다. 즉, 통계적 검정 결과도 두 회귀모형의 잔차가 stationary 하지 않음을 지지한다.
오늘은 이와 같이 시계열분석에서 회귀분석을 돌릴때에 종종 나타나는 spurious regression 문제에 대해 다뤄보았다.
그리고 그것을 판별하기 위한 하나의 방책으로써 잔차의 정상성을 확인하는것이 있음을 알게되었다.
잔차의 정상성을 확인하는 직관적인 이유는 내가 생각했을때 아래와 같다.
(그리고 좀 더 자세한 수학적 증명은 맨 아래에 있다.)

위 그림에 그려진 두 독립인 비정상 시계열을 보면 어느 순간부터는 그 추세가 바뀌는것을 확인할 수 있다. 즉 520번째 시점 전후로 A시계열은 하향추세에서 상향 추세로 바뀌며, B시계열은 상향추세에서 하향추세로 변환된다.
애초에 두 시계열은 독립이었으니 필연적으로 어느시점이후에는 갈라지는것이 분명할 것이다. 그렇기때문에 충분히 긴 시계열이라면 그 갈라지는 시점이 존재할 것이며 그 영향으로 회귀계수가 다소 뭉뚱그려질것이다. 그리고 그 여파로 잔차는 비정상이 되는 것이다. rough하게 생각하면 그렇지만 좀 더 이론적인 증명은 아래에서 진행한다.
그리고 가끔은 통계적 검정의 2종오류로 인해 위의 방법으로 spurious 관계가 식별되지 않을수도 있으므로 도메인지식으로 같이 확인하는것도 중요해보인다. 예를들면 미국의 수출 인덱스와 호주의 남성 기대 수명 간에는 인과관계가 없음을 우리는 모델을 돌려보지 않고도 알 수 있다.
+ 증명과정 )
위 예제에서 두 독립인 랜덤워크간에 회귀분석을 돌렸을때, 그 회귀모형의 잔차가 non-stationary가 나올수 밖에 없는 이유를 아래와 같이 간단하게 증명해보았다.
먼저 두 랜덤워크 중에 종속변수를 Y, 그리고 설명변수를 X라고 정의하자.
그리고 그렇게 회귀분석을 돌렸을때 아래와 같이 모델 fitting이 되었다고 하자.
$$y_{t} = c + d * x_{t} + \epsilon_{t}$$
그러면 여기서 잔차는 아래와 같이 정의된다.
$$\epsilon_{1} = y_{1} - c - d*x_{1} $$
$$\epsilon_{2} = y_{2} - c - d*x_{2} $$
$$\epsilon_{3} = y_{3} - c - d*x_{3} $$
.
.
.
그리고 Y와 X는 랜덤워크이므로 아래와 같이 데이터가 생성되었을 것이다.
$$y_{t} = y_{t-1} + \epsilon_{yt}, x_{t} = x_{t-1} + \epsilon_{xt}$$
위에서 $$\epsilon_{yt}, \epsilon_{xt}$$는 각각 t 시점에서의 X와 Y 변수에 추가될 White Noise Shock이며 $$N(0,\sigma_{y}^2), N(0,\sigma_{x}^2)$$ 을 따른다고 하자.
그렇다면
$$\epsilon_{2} = y_{2} - c - d*x_{2} = (y_{1}+\epsilon_{y2})-c-d*(x_{1}+\epsilon_{x2})= \epsilon_{1} + \epsilon_{y2} - d*\epsilon_{x2}$$ 가 되며,
$$\epsilon_{3} = y_{3} - c - d*x_{3} = (y_{2}+\epsilon_{y3})-c-d*(x_{2}+\epsilon_{x3})= \epsilon_{2} + \epsilon_{y3} - d*\epsilon_{x3}$$ 가 된다.
여기서 d는 0이 아니며, $$\epsilon_{yt} - d*\epsilon_{xt}$$ 는 $$N(0, \sigma_{y}^2 + d^2 * \sigma_{x}^2) $$ 을 따르는 White Noise가 되므로 $$\epsilon_{t} 가\,\,\,Random Walk를\,\,\, 따른다는것을\,\,\, 알 수 있다.$$
(왜냐하면 $$\epsilon_{t} = \epsilon_{t-1} + \epsilon_{yt} - d*\epsilon_{xt}$$ 의 형태를 띠기 때문에)
즉, 두 독립인 랜덤워크간의 회귀분석 결과로 나오는 잔차 역시 랜덤워크가 나오는것이다.
+ 추후 연구)
일단 증명은 두 독립인 랜덤워크 시계열 사이에서만 진행했다.
하지만, 랜덤워크 외의 비정상(non-stationary) 시계열에도 이 방법이 통하는것으로 알고 있다.
그에대한 수학적 증명도 나중에 시간이되면 진행해보면 더 개념적으로 확실해질듯 하다.
'데이터 사이언스 > Statistics' 카테고리의 다른 글
| [통계학] 시계열 분석에서 AR, MA 모형이란? (0) | 2023.02.15 |
|---|---|
| [통계학] 시계열 분석에서 stationary란 ? (0) | 2023.02.13 |
| [통계] 통계학 관련 자격증 (0) | 2022.09.16 |
| [통계학] 다중공선성은 정말로 예측력과 상관없을까? (0) | 2022.09.05 |
| 베이지안 시계열 모형 prophet (in Python) (1) | 2022.08.11 |